組み合わせ問題

中学入試で出題される「場合の数」の問題には、「組合せ」を求めるものと、「並べ方」を求める問題があります。まずは、この２つの違いを整理しましょう。

• 組合せ…順番を区別しない
• 並べ方…順番を区別する

１，２，３の３枚のカードから２枚を選ぶときで考えてみます。

• 組合せ…１と２、１と３、２と３の３通り
• 並べ方…１→２、１→３、２→１、２→３、３→１、３→２の６通り

 

並べ方は順番を区別するので、「１→２」と「２→１」は別のものと考えます。
一方、組合せは２つが何かを問うものなので「１と２」「２と１」はどちらも同じと考えます。

 

このため同じ条件（３枚のカードから２枚を選ぶなど）であれば、「組合せ」のほうが場合の数は少なくなります。では、具体的な「組合せ」問題で考えてみましょう。

 

場合の数「組合せ」問題

 

上の問題ではカードになっていますが、ボールでも人でも考え方は同じです。
７つのモノから３つを取り出す場合の数（組合せ数）は次の公式にあてはめて考えます。

 

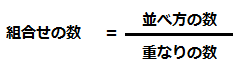
この公式を覚えていても、「並べ方の数」と「重なりの数」の求め方がわからないと意味がありませんよね。次のようにあてはめます。

 

７つのモノから３つを取り出すときの場合の数「組合せ」を求める計算式

 

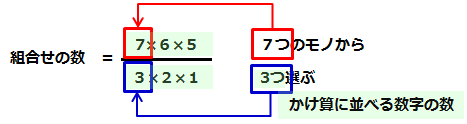
分子の「並べ方の数」には、「●つのモノから」の「●」の数字からひとつずつ引いた数をかけます。かけ算に並べる数字の数は、「▲つ取り出す（選ぶ）の「▲」の数字と同じです。

 

この問題では、７×６×５（７から１を引いた数を３つ並べたかけ算）となります。

 

分母の「重なりの数」には、「▲つ取り出す（選ぶ）の「▲」の数字ひとつずつ引いた数をかけます。かけ算に並べる数字の数は、「並べ方の数」を求めるときと同じ。

 

この問題では、３×２×１（３から１を引いた数を３つ並べたかけ算）となります。

 

あとは計算するだけ。

 

 

上の問題では、分母を見ると「３×２」がありますね。
これが分子の「６」と約分できます。

 

すると、分母は１となるので、計算は分子の７×５だけ。
７×５＝３５　が答えとなります。

 

かけ算のケアレスミスを防ぐためにも約分は必ず先にしましょう。

 

答え．３５通り