旅人算解説

算数文章題での「池の周りを二人が回る問題」の解き方を解説します。
これは旅人算と呼ばれるものです。

 

同じ方向に回る場合でも、反対方向に回る場合でも基本となる考え方は同じ。
イラスト入りで解説してますので、しっかり覚えてください。

 

池の周りをまわる二人が出会う問題の解き方

 

旅人算の出会い算と呼ばれる問題です。
池を反対方向に回るから、そのうち出会うわけですね。

 

問題文をイラスト（図）にして考えてみます。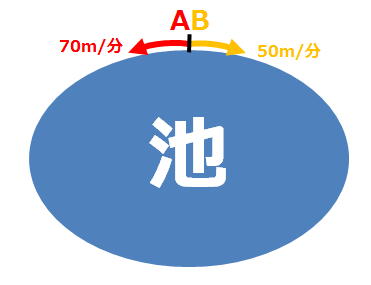

 

１分後に二人が進んだ池の周りの長さは７０＋５０＝１２０ｍです。
反対方向に進んでいる場合は、足し算の答えが二人の距離となります。

 

問題文には８分後に二人が出会ったとあります。

 

出会うというのは、上のイラストだと赤い矢印（Ａさん）とオレンジ色の矢印（Ｂさん）がぶつかることを意味します。そのとき、二人の矢印の長さの合計＝池の周りの長さとなります。

 

つまり、８分で二人が進んだ距離の合計が池の周りの長さとなります。
ココまで分かれば、カンタンですね。

 

１分後に二人が進んだ距離は１２０ｍなので、８分後なら１２０×８＝９６０ｍです。
答え．９６０ｍ

 

二人が池を同じ方向に回る問題の解き方（追い越し）

 

こちらは旅人算の追い越し算と呼ばれるものです。
追いつき算と言っても同じ。

 

早いほうが１周して、遅いほうを後ろから追い越すタイミングを求める問題です。
こちらもイラストにしてみます。

 

 

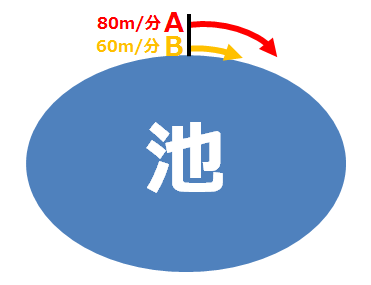
同じ方向にときの二人のあいだの距離は、速さの差になります。
赤い矢印（Ａさん）とオレンジの矢印（Ｂさん）の差が、二人のあいだに出来る距離です。

 

１分間だとＡさんは８０ｍ進み、Ｂさんは６０ｍ進みます。
このため、１分間でできる二人のあいだの距離は８０−６０＝２０ｍです。

 

この二人のあいだの距離が池の周りの長さと同じになると、ＡさんがＢさんに追いついた（追い越した）ことを意味します。

 

正確に言うと追いつくのと追い越すのでは意味が違いますが、旅人算の問題では同じ意味と考えてＯＫです（追いついて、すぐ追い越すと考えておきましょう）。

 

問題文には５０分後にＡさんがＢさんを追い越したとあります。
ということは、５０分で出来る二人のあいだの距離が池の長さとなるわけです。

 

１分で出来る二人のあいだの距離は２０ｍでした。
５０分だと、２０×５０＝１０００ｍとなります。

 

答え．１０００ｍ

 

旅人算を動画で学ぶには