

時計算の基本問題(短針と長針が重なる時刻)
中学受験の算数に出てくる時計算についての解き方の解説です。
時計算というのは、その名の通り時計の動きについて求める問題です。
いくつかのパターンがありますが、まずは最も基本的なパターンについて勉強します。

【時計算の基本問題】
3時と4時のあいだで時計の短針と長針が重なる時刻を求めなさい。
これが中学入試でも出題されたことのある時計算の基本問題です。
短針と長針が重なる時刻を求めるのは定番中の定番です。
では、解き方を順番に見ていきます。
時計算(短針と長針が重なる時刻)の解き方
実は、この問題は旅人算の中の追い越し算と同じ考え方で解くことが出来ます。
まず、旅人算(追い越し)について復習します。このような問題です。
【旅人算(追い越し問題)】
自宅から学校に向かって弟が8:00に出発し、兄は8:04分に出発しました。弟は分速80mで進み、兄は分速120mで進むとき、兄が弟に追いつくのは何時何分でしょうか?
旅人算とは、前を進んでいる人に追いつくまでの時間を求める問題です。前を進んでいる人よりも後ろの人のほうがスピードが速いので追いつくというわけです。時計算も同じです。
短針と長針が重なるというのは長針が短針に追いつくことを意味します。
速度も短針と長針では、長針のほうが速く進みますね。
違いは速度が問題文に書かれていないこと。
ただし、時計なので短針と長針の進む速度は決まっています。
| 短針 | 1分間に0.5°進む |
|---|---|
| 長針 | 1分間に6°進む |
短針が何時を表し、長針が何分を表します。
時計算では進むスピードを角度で考えます。
長針は1周(360°)で1時間(60分)なので、1分だと6°(360÷60分)。
短針は1時間に30°(360°÷12時間)なので、1分だと0.5°となります。
旅人算を解くのに、速さのほかに必要なのは2つの間の距離。
これも時計算では角度で考えます。
問題文は「3時と4時の間で…」となっています。ということは開始(スタート)は3時。このときの短針と長針の距離(角度)を求めます。
3時のときの短針と長針の角度は90°です。
(短針が1時間で30℃進むので、3時は30℃×3=90°)
ここまでを整理すると、問題が旅人算と同じになります。
- 短針と長針のあいだの距離は90°
- 短針は1分で0.5°進む
- 長針は1分で6°進む
この条件で長針が短針に追いつく時刻を求めれば答えとなります。
条件から1分間で縮まる距離は5.5°(6°−0.5°)
90°の距離を縮めるのに必要な時間は 90°÷5.5°=16と4/11
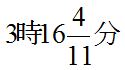
答え
時計算の練習問題
4時と5時のあいだで時計の短針と長針が重なる時刻を求めなさい。
正解・解説を表示
このタイプの時計算は問題を整理して旅人算(追越し算)の問題として解きます。
整理すると…
- 短針は1分で0.5°進む
- 長針は1分で6°進む
- 短針と長針のあいだの距離は120°
短針と長針の進む角度(速さ)は時計算の公式で覚えましょう。
4時と5時のあいだなので、4時ちょうどのときの短針と長針の角度を求めます。
30°×4=120°となります。(短針が1時間で30℃進むことから)
1分間で5.5°(6°−0.5°)だけ距離が詰まるので、120°詰まるには、
120°÷5.5°=21と9/11
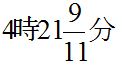
答え.
特殊算を動画で学ぶには

