

ニュートン算で定番のポンプ問題

ニュートン算の中で「ポンプ問題」といわれる問題の解き方解説です。
ポンプ問題とは、ポンプ(水道でも同じ)でプールや水そうに水を入れながら、水を抜くときに、どのぐらいでプールや水そうが空っぽになるのかといった問題です。
実際の問題を見てみましょう。
【ニュートン算のポンプ問題】
360リットルの水が入っている水そうに毎分20リットルの水をポンプで入れながら、同時に一定の割合で別のポンプから水を抜いていると、水を入れ始めてから12分で水そうが空っぽになりました。毎分何リットルの水を抜いていたのでしょうか?
ニュートン算ポンプ問題の解き方
上に書かれている問題の内容は理解できましたか?
ニュートン算は問題文が長くなる傾向にあります。
まずは、図にして問題を正しく理解しましょう。
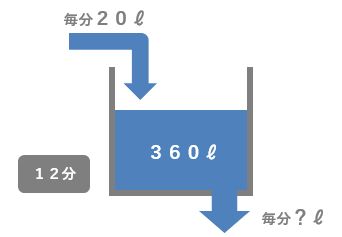
- 水そうに360リットルの水が入っている
- ポンプから毎分20リットルの水を入れる
- 別のポンプから一定の割合(毎分?リットル)の水を出す
- 12分で水そうの水が空っぽになる
長い文章もこうして図にするとわかりやすくなると思います。
では、解いていきましょう。
ニュートン算のポンプ問題を考えるときは、まず最初に次の5つを整理することが大切です。問題文にある数字もあてはめて整理します。
| もとの量 | 出る量 | 入る量 | 差(出−入) | 時間 |
|---|---|---|---|---|
| 360リットル | ? | 毎分20リットル | ? | 12分 |
差(出−入)とは、出る量から入る量を引いた差のことです。
上の表の中の「?」を求めれば、自然とそれが答えになります。
「?」は2つ。
「出る量」と「差(出−入)」です。
数字が入っているほかのところから計算でこのどちらかを求めることができます。
わかりますか?ちょっと考えてみましょう。
ニュートン算ポンプ問題の解答
360リットルあった水そうの水が12分で空っぽになったのです。
ということは、1分あたりに減った水の量が計算できますね。
360÷12=30リットル。
毎分30リットルの割合で水が減っているということです。
これが表では「差(出−入)」にあたります。
出る量と入る量の差が、水が減った量となるからです。
| もとの量 | 出る量 | 入る量 | 差(出−入) | 時間 |
|---|---|---|---|---|
| 360リットル | ? | 毎分20リットル | 毎分30リットル | 12分 |
こうなれば「出る量」はカンタンに計算できますね。
出る量−20=30なので、出る量は50リットル。
これが答えとなります。
答え.毎分50リットル
上の問題文では、「出る量」がわかりませんでしたが、「入る量」がわからない場合でも、考え方や解き方は同じです。表にして整理すれば、解けます。
ポイントは、もとの量を時間で割ると、出る量と入る量の差になるということです。
公式として覚えておきましょう。
【ニュートン算ポンプ問題(水がなくなる)の公式】
もとの量 ÷ 時間 = 出る量 − 入る量
水そうの水がなくなる場合は、出る量のほうが入る量より多くなるので、「出る量−入る量」が差となります。


