中学受験の算数文章題教室
旅人算問題の解き方
中学受験の算数で出てくる旅人算（たびびとざん）について解説しています。
「旅人算」とは、速さや時間、距離の関係を利用して、2人の移動に関する問題を解く問題です。旅人算の典型的な問題には、「出会い算」と「追いかけ算（追いつき算）」があります。
旅人算（たびびとざん）と呼ばれるわけ
旅人（たびびと）とは、文字の通り旅をしている人のことです。別々に旅をしている2人がいつ（またはどこで）出会うかという問題から旅人算と呼ばれるようになりました。中学入試で出題されるときは旅人ではなく、弟と姉のように登場人物が変わりますが、解き方（考え方）は同じです。
最も基本となる旅人算の問題はお互いに向かって進んでいる（旅をしている）二人がいつ出会うかというものです。
問題文には二人のあいだの距離とそれぞれの進む速さ（スピード）が提示されていて、ここから出会う時間を求めるというものです。具体的には、次のような問題です。
基本の旅人算：出会い算の問題
【旅人算の例題】
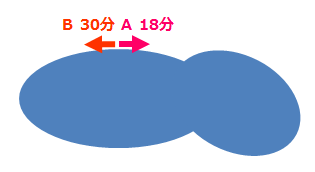
Ａ町とＢ町は１ｋｍ離れています。
兄がＡ町からＢ町に向けて分速１２０ｍで向かい、同じ時刻に弟はＢ町からＡ町に向けて分速８０ｍで向かいました。兄と弟は何分後に出会うでしょうか？
この問題は旅人算の中でも出会い算と呼ばれる種類の問題です。
これには公式があります。
【出会い算の公式】
二人が出会う時間＝二人の距離÷二人の速さの和
ポイントは二人が出会うということを二人のあいだの距離がゼロになると考えることです。上の例題にあてはめて考えると、どのような解き方になるかはこちらの解説ページ（旅人算（出会い算）の解き方）を見てください。
追いかけ算と呼ばれる旅人算
旅人算の中には二人がいつ出会うかという問題のほかに、いつ追い越すかという問題もあります。その名の通り追いかけ算と呼ばれます。
追い越すということは、二人が同じ方向に向かって進んでいるということ。
後から来る人のほうがスピードが速いので追い越すことになるのです。
この問題にも公式があります。
【追いかけ算の公式】
二人が出会う時間＝二人の距離÷二人の速さの差
二人の速さの「差」となっているところが出会い算との違いです。
例えば、このような問題です。
【追いかけ算の問題】
自宅から学校に向かって妹は８：００に出発し、兄は８：０４分に出発しました。妹は分速８０ｍで進み、兄は分速１２０ｍで進みます。兄が妹に追いつくのは何時何分でしょうか？
解説ページ⇒追いかけ算（旅人算）の解き方解説
応用問題：池の周りの旅人算
旅人算の中には池の周りをまわるパターンの問題もあります。
このパターンの問題は距離が明示されていないことが特徴です。
旅人算の公式
旅人算には、「出会い算」と「追いかけ算」があり、それぞれに公式があります。
【旅人算（出会い算）の公式】
二人が出会う時間 ＝ 二人のあいだの距離 ÷ 二人の速さの和
【旅人算（追いかけ算）の公式】
二人が出会う時間 ＝ 二人のあいだの距離 ÷ 二人の速さの差
ちがいは、二人の速さの和で割るか差で割るかです。
両方とも考え方は同じです。二人が出会う（追いつく）ということは二人のあいだの距離がゼロになるということです。
つづきは下記のページで解説しています。
