中学受験の算数文章題教室

中学受験の算数で知っておきたい公式

中学入試の算数問題で使える公式をまとめています。
鶴亀算、旅人算などの特殊算の中には公式を知らないと解けない問題や解くのに時間が掛かりすぎてしまう問題もあるので、しっかりマスターして使いこなせるようにしておきましょう。
ツルカメ算で使える公式
ツルの数 = (頭数 × 4 − 足の合計) ÷ 2
頭数というのは、ツルとカメの合計の頭数です。
足の合計もツルとカメの足の合計のこと。
全部がカメだったらと考えてツルの数を計算しているので、最初に4(カメの足の数)をかけています。最後の「÷2」はカメがツルに代わることで減る足の本数を意味しています。
旅人算で使える公式
旅人算には、二人が正反対の方向に進んで出会う時間を求める「出合い算」と同じ方向に進んで後ろの人が前の人に追いつく「追越し算」があります。
【出会い算】
- 二人が出会う時間 = 二人のあいだの距離 ÷ 二人の速さの和
【追越し算】
- 後ろの人が追いつく時間 = 二人のあいだの距離 ÷ 二人の速さの差
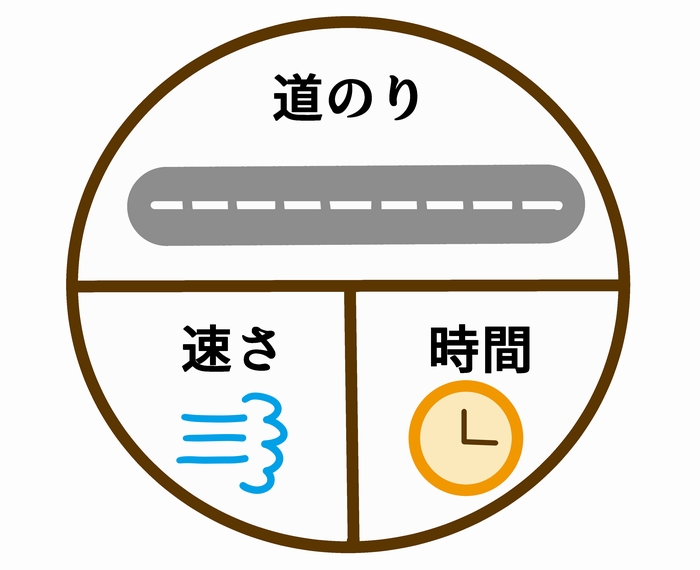
速さの問題で使える公式
速さの問題で基本となるのは、「速さ」「時間」「距離」の関係です。
- 速さ = 距離 ÷ 時間
- 時間 = 距離 ÷ 速さ
- 距離 = 速さ × 時間
3つありますが、1つ覚えておけば、2つは導き出せます。
わかりやすい数字にして覚えておくと覚えやすいです。
時速2キロ で 3時間 進むと 距離は6キロになる。
距離(6キロ) = 速さ(時速2キロ) × 時間(3時間) となります。
コレを覚えておけば、速さを求めるのであれば、答えが時速2キロとなる計算方法なので、6÷3(距離÷時間)で速さが求まると分かります。
食塩水の問題で使える公式
算数の文章題で定番の食塩水の問題を解くために必要な公式について解説しています。
食塩水の問題は複雑なものもありますが、基本となる考え方はこの公式にあります。
食塩水の問題を解くために絶対に覚えなければならない公式は次の1つです。
![]()
食塩水の濃度を求める式です。
食塩の重さを食塩水の重さで割って、100を掛けたものが濃度(%)になります。