道のり（距離）が問題文にない旅人算の解き方

旅人算の問題には次のように道のり（距離）が問題文に書かれていないものもあります。

【道のりがない旅人算の問題】
池の周りを同じ場所からＡさんは時計回りに、Ｂさんは反時計回りに回ります。Ａさんが池を１周する時間は１８分、Ｂさんが池を１周する時間が３０分のとき、ＡさんとＢさんは同時に出発してから何分後に出会いますか？

図にすると下記のようになります。

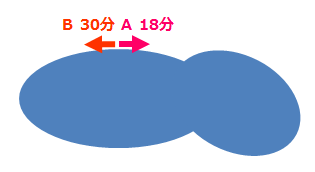
ＡさんとＢさんが同時に出発して何分後に出合うかという問題です。

「池の周りを１周する」のであれば池の形は関係ありません。丸でなくても楕円でも図のようにデコボコがある形でも同じです。ただ、この問題には池の周りの長さが書かれていません。

どのように解けばよいのでしょうか？

問題文を整理します。

まず、この「１８」と「３０」の最小公倍数を求めます。
最小公倍数の求め方は覚えていますか？

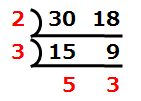
２つの数字を並べて、共通する数で割って行くのです。
２つの数字を割れる数字がなくなるまで続けます。

最後に外側の数字（赤い字の部分）をかけたのが最小公倍数です。
２×３×５×３＝９０。

この最小公倍数を「仮の」道のりとするのです。

上の例では「９０」が「仮の」道のり（距離）となります。
あくまで「仮の」道のりなので、単位は関係ありません。

単位がないとわかりにくいのであれば、ｋｍでもｍでもｃｍでも好きな単位をつけておきます（以降は説明のために距離の単位としてｋｍをつけます）。

仮の道のりが９０ｋｍだということがわかりました。
これを問題文にあてはめると、次のようになります。

ここから、１分あたりだと、どのぐらい進むかを求めます。

ココまでを整理すると、次のような問題と同じであることがわかります。

【読み替えた旅人算の問題】
１周９０ｋｍある池をＡさんとＢさんが同じ場所から反対方向に向かって同時にスタートします。Ａさんは１分間で５ｋｍ進み、Ｂさんは１分間で３ｋｍ進むとすると、二人が出会うのは出発してから何分後ですか？

こうなると通常の旅人算と同じですね。
反対方向に進む場合は速さの和が二人のあいだの縮まる距離となります。

この場合、５＋３＝８ｋｍが１分ごとに縮まる距離です。
反対方向に向かうということは、二人のあいだの距離は１周＝９０ｋｍです。

二人のあいだの距離が０になれば、二人は出会うので、それまでの時間は
９０ｋｍ÷８ｋｍ＝１１．２５分。

これが答えとなります。
答え．１１．２５分後

問題を解くときに途中で距離の単位を「ｋｍ」にしましたが、「ｍ」にしても「ｃｍ」にしても、答え＝１１．２５分後は同じです。なので、仮の道のりの単位は関係ないというわけです。

旅人算解説