

ニュートン算の基本問題と解き方を解説

ニュートン算初心者のための基本問題と解き方解説です。
「ニュートン算ってナニ?」と思っている人は、まずは問題を見てみましょう。
ニュートン算の基本問題
受付開始前に40人が並んでいて、さらに受付開始後にも一定の割合で人が並ぶ列に加わっています。受付スタート後、20秒で1人が受付を通過します。列に並んでいる人がいなくなるまでに40分かかったとすると、受付開始後に列に並んだ人は1分あたり何人だったでしょうか?
これがニュートン算の基本問題です。
「基本」でも文章が長い!
それがニュートン算の特徴です。
文章が長いときは、図にしてイメージを持つことが大切です。
上の問題文を図にして考えてみます。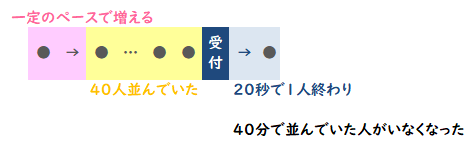
- もともと40人が並んでいる
- 受付は20秒で1人が通過
- 一定の割合で列に人が増えている
- 全部終わるまでに40分
- 【求めるもの】…1分あたり何人が列に加わったか
問題が整理出来たら、さっそく解いてみます。
上の問題文では単に「受付」としていますが、中学入試問題では「銀行の窓口」や「競技場の入り口」や「駅の自動販売機」などいろいろなパターンで出題されます。
ニュートン算基本問題の解き方
この問題では、まず「受付は20秒で1人が通過」と「全部終わるまでに40分」から、全部で何人が受付を通過したかを求めます(解説風に言うと「全体の仕事量を求める」ってヤツです)。
20秒で1人が通過ということは1分だと3人。
全部終わるまでに40分なので、3×40=120人が通過したことになります。
で、この120人のうち40人は最初から並んでいた人です。
(問題文に書いてありますよね。)
ということは、120人−40人=80人が受付開始後に列に並んだ人の数になります。80人が一定の割合で列に加わった人の数です。
「すべて終了するまでに40分」と問題文にあります。
80人が40分で列に加わったということです。
であれば、【求めるもの】1分あたり何人が列に加わったかが計算できますね。
80÷40=2人
答え.2人
どうですか?これがニュートン算です。
問題文が長い割にはあっさり解けたと思いませんか。
そうなんです。
ニュートン算は解き方さえ知っていれば、実はカンタンなんです。
ただ、初めて見るタイプの問題だと、どこから手をつけたらよいのか迷ってしまいます。ぜひ、ちがうパターンの問題にも挑戦してみてください。

