知っておきたい受験算数の特殊算で使える公式中学受験の特殊算で使える公式を一覧形式でまとめました。このページではツルカメ算、旅人算、流水算を対象としています。和で割るのか差で割るのか(旅人算)、足すのか引くのか(流水算)など混同しないように整理して覚えておきましょう。ツルカメ算で使える公式ツルの数 = (頭数 × 4 − 足の合計) ÷ 2頭数というのは、ツルとカメの合計の頭数です。足の合計もツルとカメの足の合計のこと。全部がカメだったらと考えてツルの数を計算しているので、最初に4(カメの足の数)をかけています。最後の「÷2」はカメがツルに代わることで減る足の本数を意味しています。旅人算で使える公式旅人算には、二人が正反対の方向に進んで出会う時間を求める「出合い算」と同じ方向に進んで後ろの人が前の人に追いつく「追越し算」があります。【出会い算】二人が出会う時間 = 二人のあいだの距離 ÷ 二人の速さの和【追越し算】後ろの人が追いつく時間 = 二人のあいだの距離 ÷ 二人の速さの差似たような式ですが、違いは速さの和で割るか差で割るか。出会い算は反対方向に進んでいるので、お互いの速さの和が縮まる距離と等しくなります。追越し算は同じ方向に進んでいるので、速さの差だけ距離が縮まります。このことを式で表したのが上の公式です。流水算で使える公式流水算というのは船が川を上ったり下ったりするときの時間や速さを求める問題です。川を上るというのは川の流れと反対に進むことです。船が川を上る場合の速さ = 船の速さ − 川の流れの速さ船が川を下る場合の速さ = 船の速さ + 川の流れの速さ違いは川の流れの速さを足すのか引くのかだけ。船が川を上るというのは川の流れと反対に進むということです。川の流れの分だけ戻されるので、船の速さからその分を引くというわけです。
中学受験の算数文章題教室
「 公式 」の検索結果
-
-
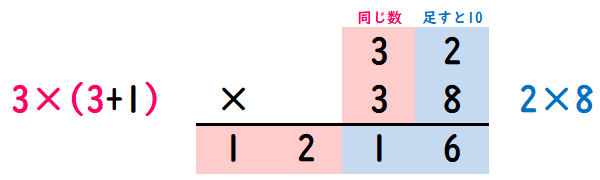
植木算、和差算、相当算で使える公式中学受験の特殊算で使える公式を一覧形式でまとめました。このページでは植木算、相当算、和差算を対象としています。特殊算は単独で出題されるだけでなく、ほかの特殊算と組み合わせて出題されることもあります。和差算は特にその傾向があるのでしっかり覚えておきましょう。植木算で使える公式同じ間隔で木を植えたときの木の数を求めるのが植木算です。木を植えるのではなく、道路に電柱と立てるというパターンもあります。使える公式は3つ。「両端に木を植える」「両端に木を植えない」「円形に木を植える」で、それぞれ公式が異なります。両端に木を植えるとき … 木の数 = 木と木のあいだの数 + 1両端に木を植えないとき… 木の数 = 木と木のあいだの数 − 1円形に木を植えるとき … 木の数 = 木と木のあいだの数実際の入試問題では「木と木のあいだの数」は問題文に書かれていないこともあります。その場合は、全体の長さと木と木のあいだの長さから求めます。木と木のあいだの数 = 全体の長さ ÷ 木と木のあいだの長さ相当算で使える公式相当算で覚えておきたい公式は、もとの数を求める式です。もとの数 = 一部の数 ÷ 一部の割合例題で考えてみます。「本を全体の5分の2読んだところ、ちょうど30ページでした。全部でその本は何ページでしょうか?」本が全部で何ページかが「もとの数」になります。30ページ ÷ ( 5分の2 ) = 75ページ が答えとなります。和差算で使える公式和差算は入試問題では別の特殊算と組み合わせて出題されることが多いものです。2つの数のうち大きいほう = ( 和 + 差 ) ÷ 22つの数のうち小さいほう = ( 和 − 差 ) ÷ 2「和」は2つの数を足した値。「差」は2つの数のうち大きいほうから小さいほうを引いた値です。式を忘れてしまったときは2つの数を「1」と「3」として考えればすぐに思い出せます。「1」と「3」の和は「4」、差は「2」。(ア) 和「4」と差「2」を足して「6」、これを2で割ると「3」。(イ) 和「4」と差「2」を引いて「2」、これを2で割ると「1」。(ア)が大きいほうの数値を求める式、(イ)が小さいほうの数値を求める式です。
-
中学受験の算数に出る差集め算の公式と解き方中学受験の算数に出てくる差集め算で使える公式と解き方を解説しています。差集め算というのはひとつひとつの差から全体の個数などを求める問題です。実際の問題で見てみましょう。差集め算の解き方【差集め算の練習問題】兄と妹が同時に出発し、兄が分速80mで歩き、妹が分速60mで進むとき、二人のあいだの距離が100mになるのは何分後ですか?問題文を整理すると、兄 … 分速80m妹 … 分速60mです。ということは1分間に20mの差があることになります。差集め算というのは「差」を集めてどのくらいになるのかというもの。この問題文の差(20m)をどのぐらい集めると100mになるかを求めれば答えになります。100m÷20m=5(分)二人のあいだの距離が100mになるのは5分後となります。差集め算の公式差集め算の公式で覚えておくのはひとつひとつの差を集めると全体の差になるということです。公式ひとつの差 × 個数 = 全体の差全体の差 ÷ 個数 = ひとつの差公式を使うときのポイントは「個数」です。上にある練習問題では時間(何分後か)が個数になります。これはひとつの差というときの「ひとつ」が時間(1分)だからです。時間の問題でなく貯金の問題でも差集め算はよく出ます。【差集め算の練習問題(貯金)】姉は毎月300円貯金し、弟は毎月180円貯金します。二人の貯金額の差が600円になるのは何ヵ月後でしょうか?これも同じ公式を使って解けます。最初に求めるのは「ひとつの差」この問題での「ひとつの差」は「一ヶ月あたりの貯金額の差」です。姉300円 − 弟180円 = 120円です。問題文から全体の差は600円です。ということは個数(何か月後か)を求めると、600円 ÷ 120円 = 5ヶ月 となります。差集め算では何を公式の「ひとつの差」と「個数」にあてはめるかがポイントです。問題演習などで身につけるようにしましょう。
-
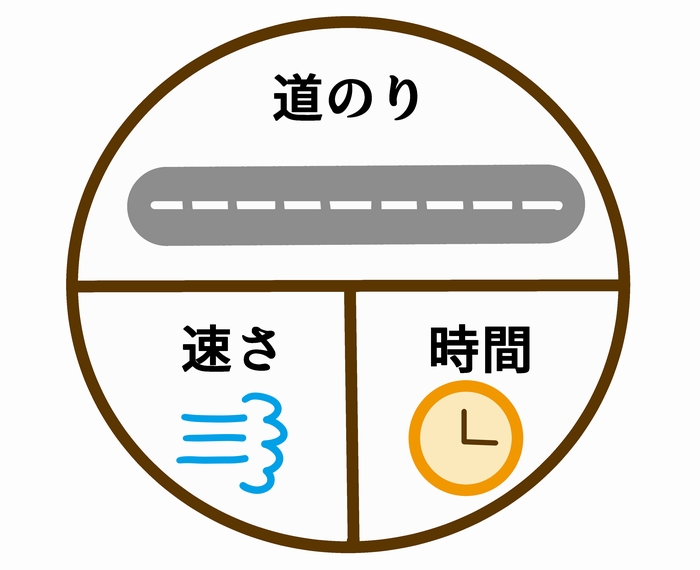
速さ、食塩水の問題で使える公式中学受験の算数の文章題でよく出てくるのが速さと食塩水の問題です。よく使う公式についてまとめました。基本的な問題でも応用問題でも公式は大切です。しっかり覚えて、使いこなせるようにしておきましょう。速さの問題で使える公式速さの問題で基本となるのは、「速さ」「時間」「距離」の関係です。速さ = 距離 ÷ 時間時間 = 距離 ÷ 速さ距離 = 速さ × 時間3つありますが、1つ覚えておけば、2つは導き出せます。わかりやすい数字にして覚えておくと覚えやすいです。時速2キロ で 3時間 進むと 距離は6キロになる。距離(6キロ) = 速さ(時速2キロ) × 時間(3時間) となります。コレを覚えておけば、速さを求めるのであれば、答えが時速2キロとなる計算方法なので、6÷3(距離÷時間)で速さが求まると分かります。食塩水の問題で使える公式食塩水の問題では濃さ(濃度)を求める公式を覚えておくことが必要です。食塩水の濃さ(%)=食塩の重さ ÷ 食塩水の重さ × 100最後の「×100」はパーセントにするために必要なものです。これも具体的な数値で覚えておきましょう。食塩が1グラム、食塩水の重さが50グラムの食塩水の濃度は2%です。濃度2% = 1グラム(食塩) ÷ 50グラム(食塩水) × 100注意しないといけないのは、食塩の重さと水の重さを足したものが食塩水の重さです。なので、50グラムの水に1グラムの食塩を加えた食塩水の濃度は2%ではありません。50グラムの水に1グラムの食塩を加えると食塩水は51グラムになります。この場合の濃度は 1グラム÷51グラム×100 で 約1.96%となります。食塩を足して濃度を求める問題では食塩水の重さも変わることを忘れないようにしましょう。ケアレスミスしがちなポイントです。気をつけてください。
-
食塩水の問題で覚えておきたい公式算数の文章題で定番の食塩水の問題を解くために必要な公式について解説しています。食塩水の問題は複雑なものもありますが、基本となる考え方はこの公式にあります。まずは基礎となるものをしっかり覚えましょう。食塩水の問題を解くために覚えておく公式食塩水の問題を解くために絶対に覚えなければならない公式は次の1つです。食塩水の濃度を求める式です。食塩の重さを食塩水の重さで割って、100を掛けたものが濃度(%)になります。これに関連して覚えておきたいことがひとつ。食塩水の重さ = 食塩の重さ + 水の重さあたり前ですが、問題を解いているときに忘れがちなので気をつけましょう。このことを使って食塩水の重さを求める問題もあります。【例題】濃度2.5%の食塩水120gに5gの食塩を加えると濃度は何%になるでしょうか?まず、濃度2.5%の食塩水120gに食塩が何グラムかを計算します。食塩式の公式では、濃度=食塩の重さ÷食塩水の重さ×100です。これを変形すると、食塩の重さ=濃度×食塩水の重さ÷100となります。例題に当てはめると、食塩の重さ = 2.5 × 120 ÷ 100 となり、3gです。注意!ここでミスしがちで、3gに5gの食塩を加えるのだから食塩は8g。食塩水の重さが120gだから…と計算するのは間違い。食塩を加えると、食塩水の重さも変わります。食塩水の重さ = 食塩の重さ + 水の重さを思い出しましょう。なので、食塩水の重さは120g+5gで125g。食塩8g(3+5)、食塩水125g(120+5)で計算します。すると、濃度 = 8 ÷ 125 × 100 で 6.4%となります。ポイントは食塩を加えると食塩水の重さも変わるということです。公式は覚えていいても、ここをウッカリしていますと計算が合いません。「食塩水の問題なんてカンタンだ」と思っている人でもケアレスミスをしがちなところなので注意しましょう。食塩水の公式まとめ濃度(%) = 食塩の重さ ÷ 食塩水の重さ × 100食塩の重さ = 食塩水の重さ × 濃度(%) × 100食塩水の重さ = 食塩の重さ ÷ 濃度(%) × 100最初の公式を覚えておけば、残り2つは導き出すことができます。
-
中学受験の算数に出る方陣算の公式と解き方中学受験の算数に出てくる方陣算の公式と解き方を解説しています。方陣算というのは、ご石やおはじきを四角形などの形にしきつめたときの、周りの個数や全体の個数を求める問題です。真ん中が空いていないのを中実方陣と呼びます。一番カンタンな正方形の中実方陣についてみていきます。【中実方陣算の練習問題】ご石を正方形にしきつめたあとで、周りのご石の数を数えると全部で28個ありました。しきつめたご石は全部で何個でしょうか。しきつめたご石の数を求めるのは、正方形の面積を求めるのと同じ。「1辺のご石の数×1辺のご石の数」で求まります。なので、「1辺のご石の数」を求めれば答えが出せます。問題文から周りのご石の数が28個なので、28÷4=7個。とするのは間違い!周りのご石の数と一辺のご石の数の関係では四隅のご石に注意しましょう。わかりやすいように一辺が3つで考えてみます。一辺が3つになるようにご石を並べると上のようになります。まわりのご石の数は8つですよね。数えてみてください。一辺の数が3つで、正方形には辺が4つあるから、3×4で12というのは間違いです。この考え方が間違いになる理由は四隅のご石を2回数えてしまうことになるから。うっかり間違いやすいので気をつけましょう。【中実正方陣算の公式】全部の数 = 1辺の数 × 1辺の数周りの数 = ( 1辺の数 − 1 ) × 41辺の数 = ( 周りの数 ÷ 4 ) + 1この公式にあてはめて上記の問題を解くと、1辺の数は、( 28 ÷ 4 ) + 1 = 8個全部の数は、 8個 × 8個 = 64個 となります。【中実方陣算の練習問題の解答】…64個方陣算には、全部の数を求める問題以外にも、周りの数を求める問題や、1辺の数を求める問題もあります。上の公式を覚えておきましょう。上の公式を忘れてしまったときは、1辺が3つの方陣算を書いて考えてみると思い出せます。テクニックとして知っておきましょう。方陣算の基本問題はコチラから【方陣算の基本問題】81個のご石を正方形にしきつめるとき、1辺に使うご石の数は何個になりますか。また、一番外側に並んでいるご石の数は合計で何個になりますか。方陣算の基本問題に挑戦!