中学入試に役立つインド式かけ算をマスター

中学入試問題でも使えるインド式掛け算を紹介します。インド式掛け算のいいところは早く正確に答えが出せるところ。計算問題が早く解けるようになれば、それだけ文章題や図形の問題に時間をかけることができます。単ねる計算術と思わずに、しっかりマスターしましょう。

 

インド式計算方法（2ケタのかけ算パート１）

２ケタ同士のかけ算で、「十の位が同じ数」かつ「一の位を足すと10」になるときに使える計算方法です（例…３２×３８）。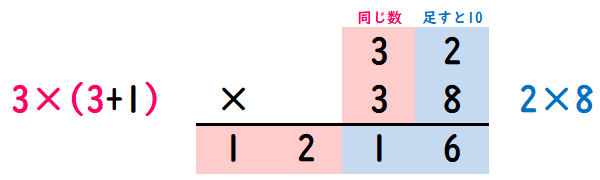

 

かけ算を２つして、数字を並べるだけで答えを出すことができます。

1. 十の位（同じ数）は、片方に１を足してかける…答えA
2. 一の位は２つの数字をかける…答えB
3. A→Bの順に並べると２ケタのかけ算の答えとなる

注意Bが１ケタとなる場合（１×９＝９）のときは、「０９」とします。
（例：３１×３９＝１２０９）

 

インド式計算方法（2ケタのかけ算パート２）

先に紹介した「パート１」の逆パターンです。２ケタ同士のかけ算で、「十の位を足すと10」かつ「一の位が同じ数」になるときに使える計算方法です（例…３６×７６）。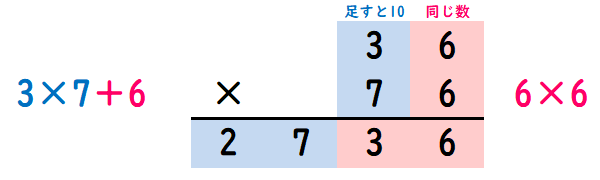

 

「かけ算を２つして、数字を並べる」のは同じですが、やり方がちょっとちがいます。

1. 十の位（同じ数）はかけた後に、「一の位の数」を足す…答えA
2. 一の位は２つの数字をかける…答えB
3. A→Bの順に並べると２ケタのかけ算の答えとなる

注意Bが１ケタとなる場合（３×３＝９）のときは、「０９」とします。
（例：２３×８３＝１９０９）

 

インド式計算方法（2ケタのかけ算パート３）

２ケタ同士のかけ算で、片方が「１１」のときもカンタンに答えを求められます。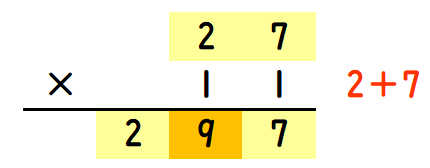

 

数字を２つにわけて、そのあいだに足した数字を入れるだけです。上の例（２７×１１）なら、２と７のあいだに２＋７の答え９を入れて、「２９７」がかけ算の答えです。

 

足した数が２ケタになるときは、その数を上のケタ（３ケタ目）に足します。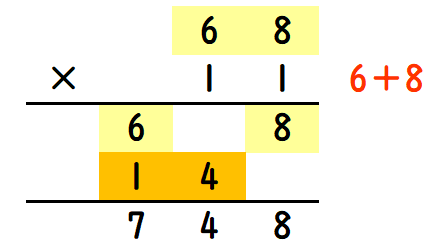

カンタンですよね。

 

中学入試で意外と出題されるので覚えておいてソンはない

中学入試で、「十の位が同じ数」かつ「一の位を足すと10」になるかけ算なんて、そんなインド式計算に都合のいい問題が出るかな？と思うかもしれませんが、意外と出ます。

 

中学入試の算数は、正攻法ですべて解こうとすると時間切れになることがあります。そこで、こうした裏ワザ的な計算方法を知っていると、時間を稼ぐことができます。

 

ここではカンタンに覚えられるものを紹介したので、ぜひ自分のテクニックとして身につけておいてください。