通過算の解き方(電柱などを通過するパターン)中学受験算数で出る通過算についての解き方の解説です。今回は通過算の中で電柱や人など長さのないものを通過するタイプの問題についてです。まずは、問題をみてみましょう。【通過算の基本問題】長さが180mある列車が電柱を通過するのに10秒かかりました。この列車の速さは秒速何mでしょうか?これが通過算の最も基本的な問題です。通過算の中には鉄橋やトンネルの中(長さのあるもの)を列車が通過する問題がありますが、その前に基本となるのがこの基本問題です。例題では「電柱を通過するのに」となっていますが、人や旗を通過する場合もあります。どちらも通過するもの(電柱、人、旗)の長さがゼロというところが共通点です。正確に言えば長さはゼロではありませんが、中学受験の算数ではゼロとみなします。(逆に、トンネルや鉄橋は長さがあります。)もうひとつの「つうかざん」中学入試に出てくる特殊算の中には通貨算(つうかざん)というものもあります。ちがいがわかりますか?通「貨」と「か」の字がちがいます。お金の「通貨」ですね。漢字で見れば間違いないと思いますが、聞いているだけではカン違いすることもあるので気をつけましょう。通過算の解き方長さがゼロなものを通過するときの速さの計算はカンタンです。速さ = 距離 ÷ 時間この問題での距離というのは電車の長さのことです。「距離=電車の長さ」と考えるのが重要ポイント!あとは問題文の数値を当てはめればOK。180m ÷ 10秒 = 秒速18m が答えです。答え.秒速18m簡単ですよね。では、練習問題では列車の長さを求める問題に挑戦してみましょう。(電車でも列車でも同じですよ。言葉の言いかえに惑わされないようにしましょう!)通過算の練習問題(電柱通過問題)秒速20mで走る列車がある電柱を通過するのに15秒かかりました。列車の長さは何mでしょうか?トンネルや鉄橋と違って電柱には長さ(幅)がありません。このため単純に距離を求める公式に当てはめることが出来ます。距離 = 速さ × 時間秒速20m × 15秒 = 300m。これがそのまま列車の長さとなります。答え.300m
中学受験の算数文章題教室
「 通過算 」の検索結果
-
-
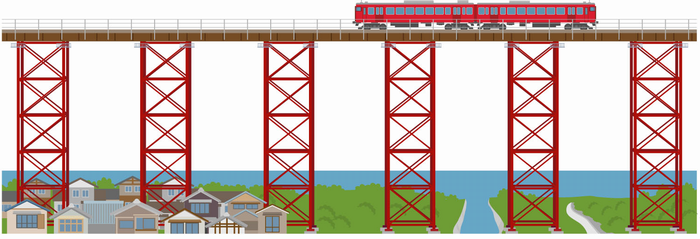
列車が鉄橋を通過する通過算の問題の解き方中学受験の算数で必須の通過算についての解き方の解説です。今回は、通過算の中で列車が鉄橋を通過するタイプの問題についてです。これもよく出題されます。まずは、問題をみてみましょう。【列車が鉄橋を通過する問題】長さが78mある列車が、300mある鉄橋を通過するのに18秒かかりました。この列車の速さは秒速何mでしょうか?例題では鉄橋となっていますが、駅のホームでも解き方は同じです。ポイントは鉄橋(駅のホーム)の長さ。長さのないもの(電柱や人)を通過する場合は、「列車の長さ÷時間」で速さが求められます。(参考記事:通過算の解き方(電柱などを通過するパターンの問題))では、長さのある鉄橋や駅のホームを通過する場合はどうでしょうか?通過算(鉄橋問題)の解き方「鉄橋を通過する」というのは、列車の先頭が鉄橋に入ってから、列車の最後尾が鉄橋を出るまでのことを指します。ポイントは、「先頭が入って、最後尾が出るまで」。「先頭が入って、先頭が出るまで」ではありません。ということは、列車が走った距離は鉄橋の長さ + 列車の長さ(先頭から最後尾まで)となります。列車の長さを足すのを忘れずに!では、公式にあてはめて考えてみます。鉄橋を通過するタイプの通過算の公式速さ = ( 鉄橋の長さ + 列車の長さ ) ÷ 時間これを問題に当てはめると、( 300m + 78m ) ÷ 18秒 = 秒速21m が答えとなります。練習問題では鉄橋の長さを求める問題に挑戦してみましょう。考え方は同じです。答え.秒速21m通過算の練習問題(鉄橋通過問題)長さが100mある列車が秒速20mで鉄橋を通過するのに16秒かかりました。鉄橋の長さは何mでしょうか?速さの公式から、距離 = 速さ × 時間です。列車が鉄橋を通過する場合は、列車の長さ+鉄橋の長さが距離になります。問題文での距離は、秒速20m(速さ) × 16秒(時間) = 320m となります。320mが、列車の長さ(100m)+鉄橋の長さ なので、鉄橋の長さは 220m となります。答え.220m
-
トンネルの中を通過する通過算の解き方中学受験算数でよく出る通過算についての解き方の解説です。今回は、通過算の中でトンネルの中を通過するタイプの問題についてです。まずは、問題をみてみましょう。【トンネルの中を通る通過算の問題】長さが120mある列車が、480mあるトンネルの中にかくれて見えなくなっている時間が20秒ありました。この列車の速さは秒速何mでしょうか?トンネルを通る通過算でポイントとなるのは、「トンネルを通過」する状態のこと。大きく2つに分かれます。(1)列車の先頭がトンネルに入ってから、列車の最後尾がトンネルを出るまで(2)列車の最後尾がトンネルに入ってから、列車の先頭が出るまで(1)の場合の解き方は、鉄橋を通過する通過算の場合と同じです。(参考記事:通過算の解き方(基本2))例題にある「トンネルの中にかくれて見えなくなっている」のは(2)にあたります。この場合の解き方を確認しましょう。通過算(トンネル問題)の解き方この問題では「列車の最後尾がトンネルに入ってから、列車の先頭が出るまで」の時間が20秒だったということになります。速さを求めるので、この時間に進んだ距離が分かれば計算できます。速さ = 距離 ÷ 時間問題は、ここでの距離です。単純にトンネルの長さではありません。必要なのは「列車の最後尾がトンネルに入ってから、列車の先頭が出るまで」に列車が進んだ距離です。「列車の最後尾がトンネルに入ったとき」に列車の先頭は、トンネルの入り口から列車の長さ分だけ進んだ位置にいます。その位置からトンネルを出るまでの長さが進んだ距離になります。ということは、列車の進んだ距離 = トンネルの長さ − 列車の長さとなり、問題文に当てはめると480m(トンネルの長さ) − 120m(列車の長さ) = 360m が列車の進んだ距離となります。この距離を20秒で進んだので、速さは360m ÷ 20秒 = 秒速18m となります。答え.秒速18m練習問題ではトンネルの長さを求める問題に挑戦してみましょう。通過算の練習問題(トンネル通過問題)秒速20mで走っている長さ100mの列車がトンネルに完全にかくれている時間が16秒でした。トンネルの長さは何mでしょうか?秒速20mで走っている列車が16秒で進む距離は、距離 = 速さ × 時間から、20m × 16秒 = 320mです。これがトンネルの長さだとすると、列車が完全にかくれることにはなりません。列車の先頭がトンネルに入って、先頭が出るまでのトンネルの長さということになります。問題文では「トンネルに完全にかくれている」とあるので、列車の最後尾までトンネルに入っていなければなりません。そのためには列車の長さ分、トンネルが長ければOKです。320m + 100m = 420m がトンネルの長さということになります。答え.420m
-
「すれ違い」「追い越す」通過算の解き方今回は通過算の中で「すれ違い」と「追い越す」問題についての解き方を解説しています。中学入試の算数では難関上位校で出題されることがい多いのでチェックしておいてください。まずは、問題をみてみましょう。【通過算(すれ違い)の基本問題】秒速20mで走っている長さ80mの列車と秒速16mで走っている長さ100mの列車が向かい合って進んでいるとき、出会ってから離れるまでにかかる時間は何秒ですか?通過算(すれ違い)の解き方これが通過算の中の「すれ違い」問題です。向かい合って進む列車が「すれ違う」のにかかる時間を求めるのが基本パターンです。「すれ違う」というのは、列車の先頭が出会ってから、列車の最後尾が離れるまでのことを指します。これは公式にあてはめて解くことが出来ます。【通過算(すれ違い)の公式】すれ違いの時間 = 2つの列車の長さの和 ÷ 2つの列車の速さの和上の問題に当てはめると、2つの列車の長さの和 = 80m + 100m = 180m2つの列車の速さの和 = 秒速20m + 秒速16m = 秒速36mとなるので、すれ違いの時間 = 180m ÷ 秒速36m で、 答えは 5秒 となります。通過算(追い越す問題)の解き方「追い越す」問題もこれと似ています。【通過算(追い抜き)の基本問題】秒速20mで走っている長さ80mの列車と秒速16mで走っている長さ100mの列車が同じ方向に進んでいるとき、追いついてから追い越すまでにかかる時間は何秒ですか?「追い抜き」問題は、速さの違う列車が同じ方向に進んでいるときに、速いほうの列車が遅いほうの列車に追いついて追い越すまでにどのくらいかかるかという問題です。追いつくというのは速いほうの列車の先頭が遅いほうの列車の最後尾に追いつくことで、追い越すというのは、速いほうの列車の最後尾が遅いほうの列車の先頭を追い越すことを指します。これも公式にあてはめて解くことが出来ます。【通過算(追い抜き)の公式】すれ違いの時間 = 2つの列車の長さの和 ÷ 2つの列車の速さの差「すれ違い」のときの公式との違いは「速さの和」で割るか「速さの差」で割るかです。「追い抜き」の場合は、「速さの差」で割ります。上の問題に当てはめると、2つの列車の長さの和 = 80m + 100m = 180m2つの列車の速さの差 = 秒速20m − 秒速16m = 秒速4mとなるので、すれ違いの時間 = 180m ÷ 秒速4m で、 答えは 45秒 となります。
-
通過算(応用問題)の解き方今回は通過算(応用問題)についての解き方の解説です。基本問題の解き方については下記ページをご覧ください。通過算の解き方(電柱などを通過するパターンの問題)通過算の解き方(列車が鉄橋を通過するパターンの問題)通過算の解き方(トンネルの中を通過するパターンの問題)では、応用問題です。【通過算の応用問題】ある列車が同じ速さで2つの鉄橋を通過しました。ひとつ目の鉄橋は長さが720mあり、列車が通過するのに40秒かかりました。ふたつ目の鉄橋は長さが405mあり、列車が通過するのに25秒かかりました。この列車の速さは秒速何mでしょうか?まず、この問題でポイントとなるのは、「列車が鉄橋を通過する」ということ。これは基本問題(2)で解説しています。思い出してみましょう。通過算(応用問題)の解き方「列車が鉄橋を通過する」というのは、列車の先頭が鉄橋に入ってから、列車の最後尾が鉄橋を出るまでのことを指します。(ポイントは先頭から最後尾まで!)ということは、列車が走った距離は、鉄橋の長さ + 列車の長さとなります。問題文にあてはめて考えると、720m+【列車の長さ】を走るのに40秒かかったということです(ひとつ目の鉄橋)。ふたつ目の鉄橋も同じように考えると…720m+【列車の長さ】 を走るのに40秒(ひとつ目の鉄橋)405m+【列車の長さ】 を走るのに25秒(ふたつ目の鉄橋)です。【列車の長さ】は同じなのでこれを除いて考えると、720m − 405m = 315m 走るのに、 40秒 − 25秒 = 15秒 かかったということになります。405mの鉄橋を通過するのに25秒かかり、それより315m長い720mの鉄橋を通過するのに40秒かかったということは、315m分を15秒で走ったと考えても同じです。315m走るのに15秒かかったときの速さは、315m ÷ 15秒 = 秒速21m(これが答えとなります。)
-
通過算の解き方で間違いやすいポイントはココ通過算には、電柱など長さのないある地点を通過する問題と、鉄橋やトンネルなど長さのあるモノを通過する問題があります。間違いやすいのは長さのあるモノを通過するときの問題です。鉄橋の通過算について例題をもとに考えてみましょう。通貨算で間違いやすいところは?【通過算の例題】長さが20mの列車が、長さ260mの鉄橋を通過するのに1分20秒かかりました。この列車の秒速を求めなさい。次の解き方には間違いがあります。どこが間違えているのかチェックしてみてください。【通過算の間違った解き方】1分20秒は80秒。鉄橋の長さ260mから列車の長さ20mを引くと240m。240m ÷ 80秒 = 3m秒答え.秒速3m列車の長さと鉄橋の長さの関係が理解できていないことによる間違いです。キレイに割り切れるので正解だと思ってしまいがちですが、気をつけましょう。通過するとはどのような意味か通過算で大切なのは「通過する」という意味を正しく理解することです。算数の問題ですが、国語力が必要というわけです。「鉄橋を列車が通過する」というのは、列車の先頭が鉄橋に入ってから列車の最後尾が鉄橋を出るまでのことです。列車の一部分でも鉄橋にあるときは、通過中です。ということは、列車の先頭部分が走る距離はどうなるでしょうか?列車の先頭が、鉄橋に入ったときから鉄橋を出るときまでは鉄橋の長さと同じ。列車の先頭が出ても、まだ列車は鉄橋を通過したことになりません。列車の最後尾が鉄橋を出るまでです。列車の最後尾が鉄橋を出るときは、列車の先頭は鉄橋から列車の長さ分だけ先に行っています。鉄橋の長さ+列車の長さが走った距離となるわけです。間違えた原因速さを計算するために、距離と時間を求める考え方はあっています。ただし、上の解き方では距離の求め方が間違っていました。足すべきところを、引いてしまったことが間違いです。正しい解き方は下記になります。1分20秒は80秒。鉄橋の長さ260mに列車の長さ20mを足すと280m。これが列車が鉄橋を通過するのに走った距離。速さは、距離÷時間だから、280m ÷ 80秒 = 3.5m秒答え.秒速3.5m文章題では問題文の数字を見たときに、計算しやすい(割り切れる)式が「見えて」しまうことがありますが、そうしたときほど要注意です。足すべきところを引いていないかなど、しっかり確認して解くようにしましょう。文章題に慣れている人ほど、こうしたケアレスミスをしがちです。入試の問題では、このような「ひっかけ」問題もあることに注意してください。通過算の間違いやすいポイント通過算では、通過するものの長さと列車の長さの関係に気をつけましょう。通過するための距離は、通過するものの長さ+列車の長さです。列車の先頭部分を基準に考えると、わかりやすいと思います。うっかり引いてしまわないようにしてください。