三角数問題

中学入試で出題される三角数の問題の解き方を解説します。

 

三角数とは、1,3,6,10,15,21…と規則的に並んだ数のことで、点（マーク）を正三角形の形に並べたときの点（マーク）の数のことです。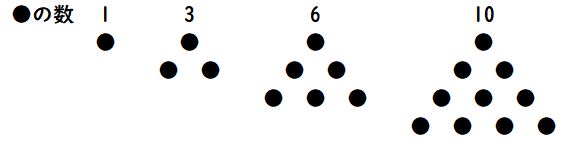

上の図で●の数（1,3,6,10）が三角数です。
中学入試問題では次のように出題されます。

 

中学入試の問題では、「三角数」という言葉を使わずに、上のように図で説明することが多くなっています。この問題の解き方を説明します。

 

三角数の例題の解き方

まずは三角数の法則に着目します。
上の図で1段目の●の数は1個、2段目は2個、3段目は3個…となっていますね。

 

また、2段目までの●の数の合計は1段目の個数＋2段目の個数。
3段目までの●の数の合計は、1段目の個数＋2段目の個数＋3段目の個数となります。

 

つまり、3段目までの●の数の合計は1＋2＋3。
4段目までの合計は1＋2＋3＋4。5段目までの合計は1＋2＋3＋4＋5となります。

 

ということは、12段目までの●の数の合計は1＋2＋3＋4＋5＋6＋7＋8＋9＋10＋11＋12です。これを順番に計算して…というのは間違いのもとですし、時間もかかります。

 

1から「ある数」までの合計は、順番に足さなくても求めることができます。

 

1から12までの合計の求め方

1から「ある数」までの合計は、同じ数になるペアを使って計算することができます。

 

数を左から順番に並べて、一番左側の数字と一番右側の数字、左から二番目の数字と右から二番目の数字を足した数は同じになります。

 

1から12までの合計なら、「1と12」「2と11」の合計はどちらも「13」です。
図にして考えると下のようになります。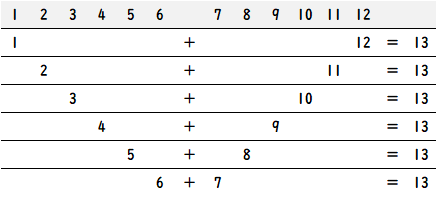

 

このように13になる組み合わせが6個できます。
ということは、13×6＝78が1から12までの合計となります。

 

1から12までの合計が12段目までに必要となる●の数なので答えは78個となります。

 

答え．78個

 

中学受験向けワンポイント（1から「ある数」までの合計）

 

三角数の例題（別パターンでの出題）

中学入試では上で見た三角数の例題が別の形式で出題されることもあります。

上の問題文では三角形の図がありませんが、これも三角数の問題です。

 

数字の並びが三角数になっていることに築きましたか？
1から始まって、＋2、＋3、＋4、＋5、＋6、＋7と数字が増えています。

 

これは三角数なので、12番目の数字を求めるというのは、最初の例題の12段目までの●の数を求めるのと同じです。

 

答え．78

 

四角数の問題と解説はコチラ