四角数問題

中学入試で出題される四角数の問題の解き方を解説します。

 

四角数とは、1,4,9,16,25,…と規則的に並んだ数のことで、点（マーク）を四角形に並べたときの点（マーク）の数のことです。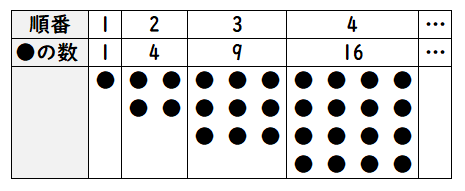

上の図で●の数（1,4,9,16）が四角数です。
中学入試問題では次のように出題されます。

 

中学入試の問題では、四角数の問題は上のような図で出題されることが一般的です。
では、この問題の解き方を説明します。

 

四角数例題の解き方

四角形に並んだ点（マーク）の数はタテの数×ヨコの数で求めることができます。

 

上の図で順番1の●の数は1個、順番2は4個、順番3は9個となっていますね。
これは「1×1」「2×2」「3×3」の答えと同じです。

 

ということは、15番目のときの●の数は「15×15」で求められます。
15×15=225

 

答え．225個

 

四角数の例題（その２）

中学入試では上の例題を逆算するような問題も出題されます。

 

？？×？？＝8464となる「？？」の数が答えとなることは最初の例題からわかるかと思いますが、この「？？」をどのように求めればよいのでしょうか。

 

まずは、答えが8464に近いおよその数を求めます。

• 100×100=10000
• 90×90=8100

このことから、？？×？？＝8464となる「？？」は90から100のあいだの数とわかりますね。
次に下１ケタの数字に注目します。

 

答えの下一ケタの数	かけた数の下一ケタ
下1ケタが１	１ または ９
下1ケタが４	２ または ８
下1ケタが５	５
下1ケタが６	４ または ６
下1ケタが９	３ または ７

 

同じ数をかけた答えが「8464」であれば、下一ケタは「4」なので、下一ケタが「2」か「8」の数をかけたことになります。

 

最初の推測で「8464となる？？×？？の？？は90から100のあいだの数」とわかっているので、これを加えると候補になるのは「92」か「98」です。

 

候補が２つなら計算してみて探すこともできますが、さらにどちらかを推測する方法もあります。

• 100×100=10000
• 90×90=8100

を思い出してください。いま求めている答えは「8464」です。10000より8100に近いですよね。ということは、92と98なら「92」のほうという推測が成り立ちます。

 

実際に計算して確認すると、92×92＝8464です。
（ちなみに、98×98＝9604です。）

 

答え．順番が92のとき